Formules et tolérances relatives aux contenances déterminées par arpentage
I. Formules mathématiques relatives a la détermination des contenances d'arpentage
A. Polygones particuliers
1. Surface d'un triangle
S = ah/2, où a représente la longueur d'un côté et h la hauteur correspondante.
S =1/2 bc sin A, où b et c représentent les longueurs de deux côtés et A l'angle formé par ces derniers.
![]() , où p désigne le demi-périmètre du
triangle et a, b et c les longueurs de chacun des côtés.
, où p désigne le demi-périmètre du
triangle et a, b et c les longueurs de chacun des côtés.
2. Parallélogramme
La surface d'un parallélogramme est égale au produit des longueurs d'une base et de la hauteur correspondante.
3. Trapèze
La surface est égale au produit de la demi somme des bases par la hauteur.
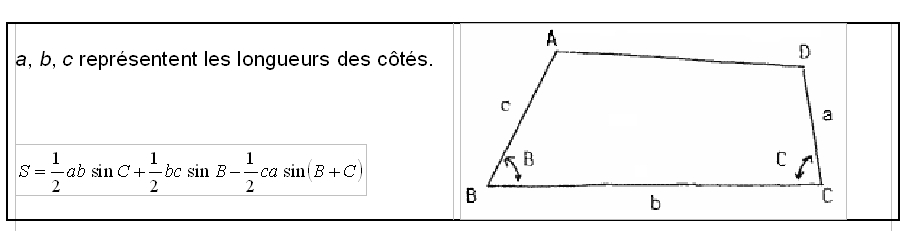
4. Quadrilatère dont on connaît trois cotes et les deux angles qu'ils forment
(cf. figure)
B. Polygones quelconques
1. Formules en fonction des coordonnées rectangulaires des sommets
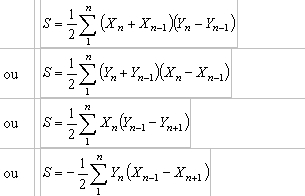
L'ordre de parcours des points du polygone est effectué dans le sens rétrograde.
2. Formules en fonction des coordonnées polaires des sommets
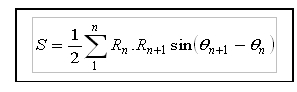
où Rn représente la distance du point de station à chaque sommet n du polygone et n la lecture angulaire effectuée sur le sommet n.
Comme dans le cas précédent, l'ordre de parcours des points du polygone est effectué dans le sens rétrograde.
II. Tolérances admissibles entre mesurages de longueurs sur le terrain et mesurages de contrôles
La tolérance est déterminée selon la formule :
![]()
où T est exprimée en centimètres et L (longueur mesurée) en mètres.
Les résultats sont regroupés dans le tableau ci-après.
Comparaison entre longueurs sur le terrain et mesurages de contrôles
Table de tolérance
|
Longueur L mesurée |
Tolérance T correspondante |
|
Inférieure à 5 |
7 |
CAD - Mise à jour du plan - Confection des documents d'arpentage - Travaux et signature
CAD – Mise à jour du plan - Confection des documents d'arpentage
CAD - Mise à jour du plan - Document d'arpentage - Vérification et renvoi des documents